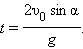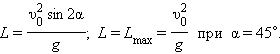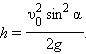17:15 Консультация №3 ЕГЭ физика 11 класс | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Блок формул №3 7 класс 21) Условие плавание тел: Если Fтяж > Fа, то тело тонет Если Fтяж = Fа, то тело плавает Если Fтяж < Fа, то тело всплывает Если ρтела > ρжидкости , то тело тонет Если ρтела = ρжидкости , то тело плавает Если ρтела < ρжидкости , то тело всплывает 22)работа A=F*S [A]=1Дж 23)мощность N=A/t N=F*v [N]=1Вт 24)Условие равновесия рычага: F1/F2 = L2/L1 25) Момент силы M=F*L , [M]=1H*м Правило моментов: M1=M2, F1*L1 = F2*L2 26) Подвижный блок F=P/2 27) кпд = Аполезная/Азатраченная *100% 28)кинетическая энергия Ек=m*v*v/2 29) потенциальная энергия Еп = mgh Еп=k*x*x/2 30) Золотое правило механики A1=A2 Механическое движение тел изучается в разделе физики, который называется механикой. Основная задача механики – определить положение тела в любой момент времени. Одна из основных частей механики, которая называется кинематикой, рассматривает движение тел без выяснения причин этого движения. Кинематика отвечает на вопрос: как движется тело? Другой важной частью механики является динамика, которая рассматривает действе одних тел на другие как причину движения. Динамика отвечает на вопрос: почему тело движется именно так, а не иначе?
1) основные понятия кинематики Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца. Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку. Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Понятие материальной точки играет важную роль в механике. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела. Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени
Перемещением тела Пройденный путь Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. ля характеристики движения вводится понятие средней скорости:
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени
Мгновенная скорость
Мгновенным ускорением (или просто ускорением)
Направление вектора ускорения
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
Вектор Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Нормальное ускорение зависит от модуля скорости
Вектор Из рис. 1.1.5 видно, что модуль полного ускорения равен
Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д. 2) относительность движения
Здесь В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными. 3) ПРД Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось Если в некоторый момент времени Эта величина может быть и положительной и отрицательной в зависимости от направления, в котором двигалось тело. При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем. Скоростью равномерного прямолинейного движения называют отношение
Если Зависимость координаты В этом уравнении
Чем больше угол 4) РУПД В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения при равноускоренном прямолинейном движении скорость тела определяется формулой
В этой формуле
По наклону графика скорости может быть определено ускорение
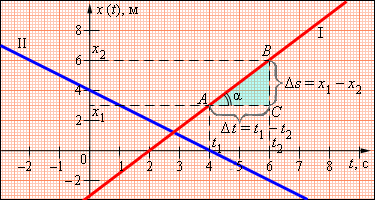
Чем больше угол График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
Так как
Для нахождения координаты
Это выражение называют законом равноускоренного движения. При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
Из этой формулы можно получить выражение для определения конечной скорости
Если начальная скорость
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины 5) Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом Простым примером свободного падения является падение тела с некоторой высоты Скорость отрицательна, так как вектор скорости направлен вниз.
Время падения
Скорость тела в любой точке составляет:
В частности, при
Пользуясь этими формулами, можно вычислить время падения тела с данной высоты, скорость падения тела в любой момент после начала падения и в любой точке его траектории и т. д. Аналогичным образом решается задача о движении тела, брошенного вертикально вверх с некоторой начальной скоростью Через время
Тело возвращается на землю ( Максимальная высота подъема
Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось
Таким образом, для движения вдоль оси а для движения вдоль оси Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом Время полета:
Дальность полета:
Максимальная высота подъема:
Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела. Задание: ЕГЭ 2016 (2017) физика, сборник заданий Н.К. Ханнанов, Г.Г.Никифоров, В.А. Орлов Раздел Кинематика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
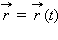 (векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).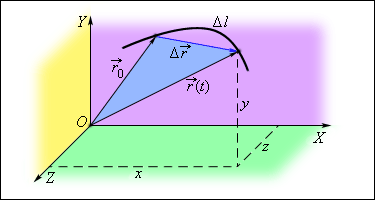
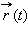 .
. 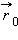 – радиус-вектор положения точки в начальный момент времени
– радиус-вектор положения точки в начальный момент времени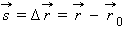 называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. 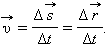
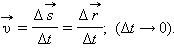
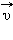 тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.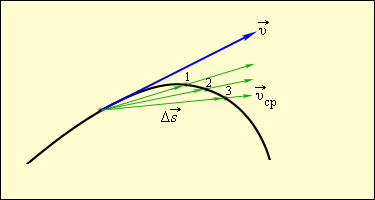
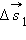 ,
, 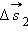 ,
, 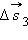 – перемещения за времена
– перемещения за времена 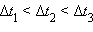 соответственно. При
соответственно. При 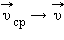
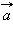 тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости 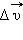 к малому промежутку времени
к малому промежутку времени 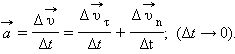
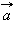 в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 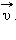 Составляющие вектора ускорения
Составляющие вектора ускорения 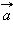 называют
называют 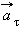 и
и 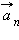 ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).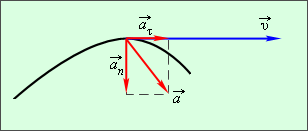
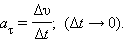
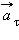 направлен по касательной к траектории.
направлен по касательной к траектории.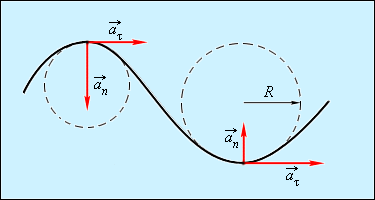
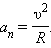
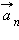 всегда направлен к центру окружности (
всегда направлен к центру окружности (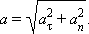
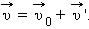
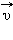 – скорость тела в «неподвижной» системе отсчета
– скорость тела в «неподвижной» системе отсчета 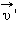 – скорость тела в «движущейся» системе отсчета
– скорость тела в «движущейся» системе отсчета 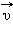 и
и 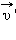 иногда условно называют абсолютной и относительной скоростями; скорость
иногда условно называют абсолютной и относительной скоростями; скорость 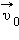 называют переносной скоростью.
называют переносной скоростью.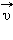 равна векторной сумме его относительной скорости
равна векторной сумме его относительной скорости 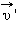 и переносной скорости
и переносной скорости 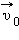 движущейся системы отсчета.
движущейся системы отсчета.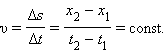
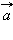 остается неизменным по модулю и направлению. изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости
остается неизменным по модулю и направлению. изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 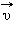 и ускорения
и ускорения 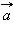 направлены вдоль прямой движения. Поэтому скорость
направлены вдоль прямой движения. Поэтому скорость 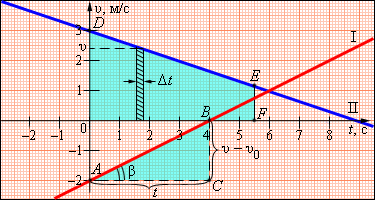
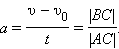
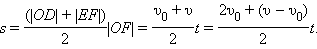
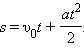
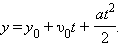
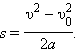
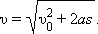
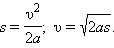
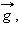 он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение
он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение 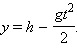
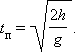
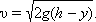
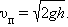
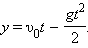
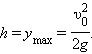
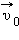 тела и его проекции на координатные оси.
тела и его проекции на координатные оси.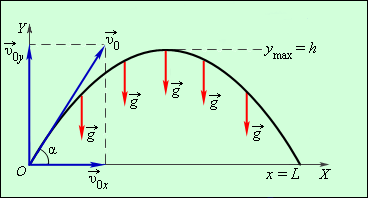
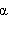 к горизонту. Разложение вектора
к горизонту. Разложение вектора 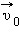 начальной скорости тела по координатным осям
начальной скорости тела по координатным осям